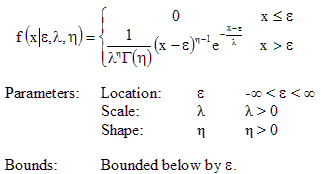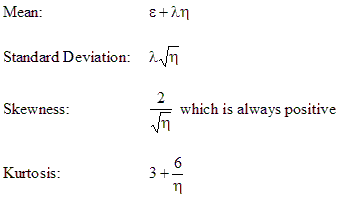Contents
- Index
Gamma Family of Distributions
Shape:
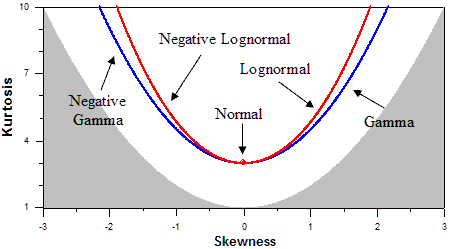
The gamma family of distributions is made up of three distributions: gamma, negative gamma and normal. It covers any specified average, standard deviation and skewness. Together they form a 3-parameter family of distributions that is represented by a curve on a skewness-kurtosis plot as shown below. The gamma distribution covers the positive skewness portion of the curve. The negative gamma distribution covers the negative skewness portion of the curve. The normal distribution handles the remaining case of zero skewness. The gamma curve falls below the lognormal curve.
Density Function:
The density function of the gamma distribution is shown below:

The equation, parameters and bounds of the density function are:
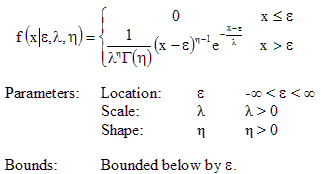
Moments:
The moments of the gamma distribution can be calculated from the parameters as shown below:
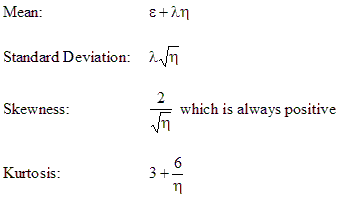
Properties:
As the skewness goes to zero, both the gamma and negative gamma distributions limit to the normal distribution. This means that in some cases the gamma and normal distributions can be difficult to distinguish between. As a result, some sets of data may fit both the gamma and normal distributions.
The exponential distribution is a special case of the gamma distribution and thus falls on the gamma curve in the skewness-kurtosis plot.