Contents
- Index
Maximum Likelihood Method
An approach to fitting a distribution to a set of data that involves maximizing the likelihood function. The likelihood function is based on the density function of the distribution. If f(x|parameters) is the density function, then the likelihood function is:
where n is the sample size and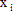 
represents the data points. The likelihood function is akin to finding the values of the parameters making the resulting data most likely (probable).
Using the maximum likelihood method always results in the data being within the range of the distribution. However, it is possible the spec limits are outside the range of the distribution and cannot be transformed.
This approach has been further adapted so that the user can specify a range of values that must be in the range of the selected distribution. This range can be specified using the Select Distribution to Fit Data dialog box. When the Find Best Distribution button is clicked in the Data window, the required range is automatically specified as at least 1 standard deviation beyond any spec limits. This assures the spec limits are also within the range of the distribution and can be transformed.
An alternative approach for fitting data is the method of moments method.